Kui soovite suletud vormis funktsiooni, annab Wikipedia need:

\ begin {align} R & = \ frac {Z_m} {2 \ pi \ sin ^ 2 (kL / 2)} \ Big \ {\ gamma + \ ln (kL) - \ operaatori nimi {Ci} (kL) + \ tfrac {1} {2} \ sin (kL) \ big [\ operaatori nimi {Si} (2kL) - 2 \ operaatori nimi {Si} (kL) \ big] \\ & \ qquad \ qquad \ qquad \ qquad + \ tfrac {1} {2} \ cos (kL) \ big [\ gamma + \ ln ( kL / 2) + \ operaatori nimi {Ci} (2kL) - 2 \ operaatori nimi {Ci} (kL) \ big] \ Big \} \\ X & = \ frac {Z_m} {4 \ pi \ sin ^ 2 (kL / 2)} \ Big \ {2 \ operaatori nimi {Si} (kL) + \ cos (kL) \ big [2 \ operaatori nimi {Si} (kL) - \ operaatori nimi {Si} (2kL) \ big] \\ & \ qquad \ qquad \ qquad \ qquad - \ sin (kL) \ big [2 \ operaatori nimi {Ci} (kL) - \ operaatori nimi {Ci} (2kL) - \ operaatori nimi {Ci} (2ka ^ 2 / L) \ big ] \ Suur \} \ lõpp {joondamine}

Ma ei hakka neid võrrandeid isegi seletama, kuna need on nii karvad. Lihtsam ja mõistlikum on näha võrrandite graafikut (samast Vikipeedia artiklist):

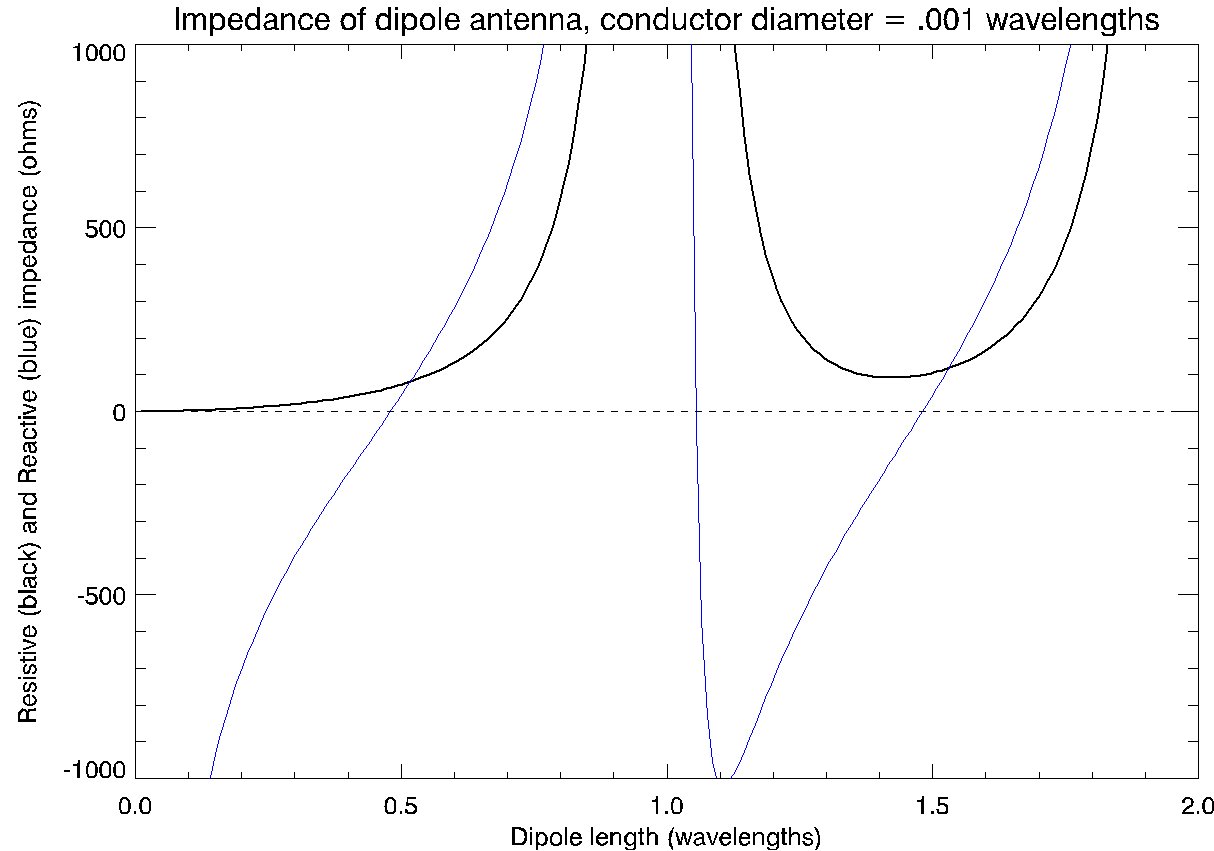
Teoreetiliselt on 5/8 monopoli impedants: midagi sellist nagu $ (75-425j) \: \ Omega $ ja dipooli impedants on kaks korda suurem kui samaväärsel monopoolil, seega $ (150-850j) \: \ Omega $. Silmamäng, mis graafikul tundub olevat õige.

Siinkohal tuleb siiski märkida, et umbes 1,25λ on impedantsi nii tegelike kui ka kujuteldavate komponentide kalle üsna järsk, mis tähendab väikseid muutusi pikkuses teha impedantsis suuri muutusi. Pange tähele ka seda, et see graafik kehtib ainult juhi läbimõõdu korral 0,001λ. Paksemad või õhemad juhid võivad samuti märkimisväärselt muutuda. Impedantsi tundlikkus nende parameetrite suhtes seletab erinevate allikate antud arvude erinevusi.

Seetõttu on selle antenni edukaks ehitamiseks vaja impedantsi mõõtmiseks ja vastavalt kohandamiseks mingit viisi.

Takistus on 5/8 laine monopooliga võrreldes topelt, mida on hästi uuritud, seal on palju teavet.

ARRL-i antennikogust:

"5/8-lainelise piitsa sisendtakistusel üle läbimõõduga 1/2 lainepikkusega maapinna on takistuslik komponent, mis on lähedal 50 oomi ja mahtuvuslik reaktants, mis sõltub oluliselt piitsa läbimõõdust, tavaliselt vahemikus 50 kuni 150 oomi.

Teie 1,25 lainepikkusega dipooli impedants on umbes 100 -j100 kuni -j300 oomi.

Selle antennivaliku kohta on kaks kommentaari:

• suurem võimendus tähendab suuremat võimsust ainult siis, kui suunate antenni allikale. Kui tavaliselt koristate, kasutage pigem väikese võimendusega antenni.
• see on üsna kitsa ribaga antenn, seega on see tõesti kasulik ainult siis, kui teate korjatava signaali sagedust. Selle takistus muutub sagedusega kiiresti ja sobivad induktiivpoolid muudavad teist teed.